English
1537. Get the Maximum Score 
Problem Statement:
You are given two sorted arrays of distinct integers nums1 and nums2.
A valid path is defined as follows:
- Choose array
nums1ornums2to traverse (from index-0). - Traverse the current array from left to right.
- If you are reading any value that is present in
nums1andnums2you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The score is defined as the sum of uniques values in a valid path.
Return the maximum score you can obtain of all possible valid paths. Since the answer may be too large, return it modulo 109 + 7.
Example 1:
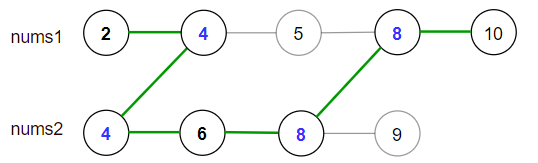
Input: nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
Output: 30
Explanation: Valid paths:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10], (starting from nums1)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (starting from nums2)
The maximum is obtained with the path in green [2,4,6,8,10].
Example 2:
Input: nums1 = [1,3,5,7,9], nums2 = [3,5,100]
Output: 109
Explanation: Maximum sum is obtained with the path [1,3,5,100].
Example 3:
Input: nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
Output: 40
Explanation: There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path [6,7,8,9,10].
Constraints:
- 1 <= nums1.length, nums2.length <= 105
- 1 <= nums1[i], nums2[i] <= 107
- nums1 and nums2 are strictly increasing.
Solution:
java
public class GetTheMaxScore {
/* Two Pointer Approach */
public int maxSum(int[] nums1, int[] nums2) {
// initializing two pointer vars
int i = 0, j = 0;
int len1 = nums1.length, len2 = nums2.length;
// taking the vars of long type to avoid integer overflow or runtime error
long upperSum = 0, lowerSum = 0;
// traverse till one of the arrays length
while (i < len1 && j < len2) {
// adding the element to the upperSum until element of first array is >=
// the element of second array & then increamenting the pointer var by 1
if (nums1[i] < nums2[j])
upperSum += nums1[i++];
// adding the element to the lowerSum until element of second array is >=
// the element of first array & then increamenting the pointer var by 1
else if (nums1[i] > nums2[j])
lowerSum += nums2[j++];
// when the element of both arrays are equal,
// assign the value of max of upperSum & lowerSum and adding the element itself
else {
upperSum = lowerSum = Math.max(upperSum, lowerSum) + nums1[i];
// increasing both pointer by 1, as the value at both the pointers is same,
// avoiding the repetition of element in the sum
i++;
j++;
}
}
// adding the remaining element from first array
while (i < len1)
upperSum += nums1[i++];
// adding the remaining element from second array
while (j < len2)
lowerSum += nums2[j++];
return (int) (Math.max(upperSum, lowerSum) % 1000000007);
}
}
...
